One of the earliest mathematical modeling questions our group began working concerned how we should best deploy antimalarial therapies to delay the onset of drug resistance for as long as possible. This is a “resistance management” problem, and you can find some of the earliest publications on this topic here and here. This work was led by Tran Dang Nguyen, and Nguyen did all the initial C++ model development and epidemiological, pharmacological, and clinical validation during the first years of his PhD studies.
The individual-based model that Nguyen developed simulates a scenario of malaria endemicity for twenty years, allowing for drug-resistant mutants to emerge and cause epidemics of drug-resistant malaria. The drugs used to treat symptomatic malaria in the simulation are the three artemisinin combination therapies (ACTs): artemether-lumefantrine (AL), artesunate-amodiaquine (ASAQ), and dihydroartemisinin-piperaquine (DHA-PPQ).
Our analysis compared three different ways of deploying these ACTs. The first is as part of a five-year cycling scheme, where one therapy is used as first-line for all malaria cases for five years, after which it is rotated out for another ACT. The second is a cycling or “sequential deployment” scheme where the therapies are rotated out once they reach 10% treatment failure (in this scheme a one-year delay is implemented before a switch occurs). And the third method is to deploy multiple first-line therapies (MFT) where all of the ACTs are distributed at the same time in equal proportions.
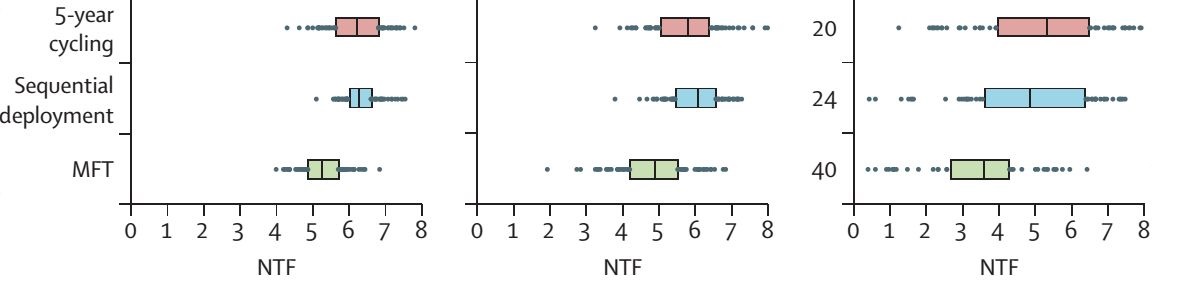
The interquartile ranges above show summaries of simulation output. The treatment coverage increases from 50% to 60% to 70% from left to right in the panels. And the x-axis shows the Number of Treatment Failures (NTF) per year per 100 population during the 20-year simulation, discounted at 3% annually. The strategy that minimizes drug resistance results in the fewest long-term number of treatment failures.
You’ll notice that the rightmost panel has a few extra numbers on the side. These are the numbers of simulation runs, out of 100, that reached elimination (i.e. zero malaria).
The scenarios above were run in a low transmission setting of 1.3 infectious bites per person per year. In our paper and supplement you can see results for a range of scenarios, including different coverage levels, different transmission settings, and different biological fitness costs for drug-resistant genotypes. Across the most comprehensive set of scenarios that we ran, MFT outperformed the two cycling strategies 86% of the time, and the median reduction in treatment failures was 10%.
There are three main reasons that MFT strategies outperform cycling strategies when it comes to preventing drug resistance. The first is that simultaneous deployment of different drugs or therapies in a population forces a pathogen to adapt to a variable environment; cycling strategies do not create the same degree of variability because only one drug is deployed at a time. This principle was described very clearly and demonstrated with the use of a simple mathematical model by Bergstrom et al. The second reason is that cycling strategies erode the mean fitness of the pathogen population more quickly — by allowing rapid resistance evolution to a single drug to occur — and this lower mean fitness allows future drug-resistant genotypes to establish more easily. This point requires a bit of quiet thinking and diagramming, and a good illustration to start with is Figure 5 in this paper. The third reason can be seen in Figure 1 of our current paper. Cycling strategies can be associated with epidemiological rebounds. This means that an epidemic of drug-resistant malaria can gather enough momentum to overshoot its natural equilibrium and cause higher-than-expected malaria case loads for a number of years.
The computational and theoretical arguments point to the simultaneous deployment of antimalarial drugs as the best way to delay and slow down drug resistance. More work remains to be done on the communication and operations side of this major public health question. Our hope is that 2016 and 2017 will see some progress in this area.
Two editorials that commented on multiple first-line therapies can be found here and here.
And you can listen to the Lancet Global Health’s short podcast here.
The C++ source code for the individual-based simulation model is available on Github.